Why and when cascading filters is bad! [Heavi]
It is perhaps common knowledge amongst RF engineers that directly cascading filters is not appropriate. One cannot simply assume that adding two filters front-to-back is equivalent to combining (adding) their filter characteristics.
If we think about ladder networks of LC components (Chebychev filters) for example this becomes very obvious. If it where as simple as simply adding the filters you could design an 8th order filter by simply cascading 4 of the same second-order filters front-to-back and be done.
It is also however true to say that cascading filters can work reasonably well! In the following example I simulate two realizations of simple RF networks. In the first case I have two 5th order Chebychev band-stop filters front-to-back with a 100MHz bandwidth. One sits at 2GHz and the other at 2.3GHz. The two filters are separated by 5mm of slightly mismatched transmission line (51 ohms instead of 50 ohms). In the second case I just have the one filter at 2GHz (same properties).
I can fairly easily set this simulation up in Heavi.
import heavi as hv
f = hv.frange(1.8e9, 2.5e9, 2001)
# Model with two cascaded filters
model = hv.Model(suppress_loadbar=True)
p1 = model.port(50)
p2 = model.port(50)
n1 = model.node()
n2 = model.node()
model.filters.cauer_filter(model.gnd, p1, n1, 2e9, 100e6,
5, 0.05,
hv.FilterType.CHEBYCHEV,
type=hv.BandType.BANDSTOP,
chebychev_correction=False)
model.filters.cauer_filter(model.gnd, n2, p2, 2.3e9, 100e6,
5, 0.05,
hv.FilterType.CHEBYCHEV,
type=hv.BandType.BANDSTOP,
chebychev_correction=False)
model.transmissionline(model.gnd, n1,n2, 51, 2.1, 0.005)
S = model.run_sparameter_analysis(f)
# Model with one filter
model2 = hv.Model(suppress_loadbar=True)
p12 = model2.port(50)
p22 = model2.port(50)
model2.filters.cauer_filter(model2.gnd, p12, p22, 2e9, 100e6,
5, 0.05,
hv.FilterType.CHEBYCHEV,
type=hv.BandType.BANDSTOP,
chebychev_correction=False)
S2 = model2.run_sparameter_analysis(f)
# Plotting the data
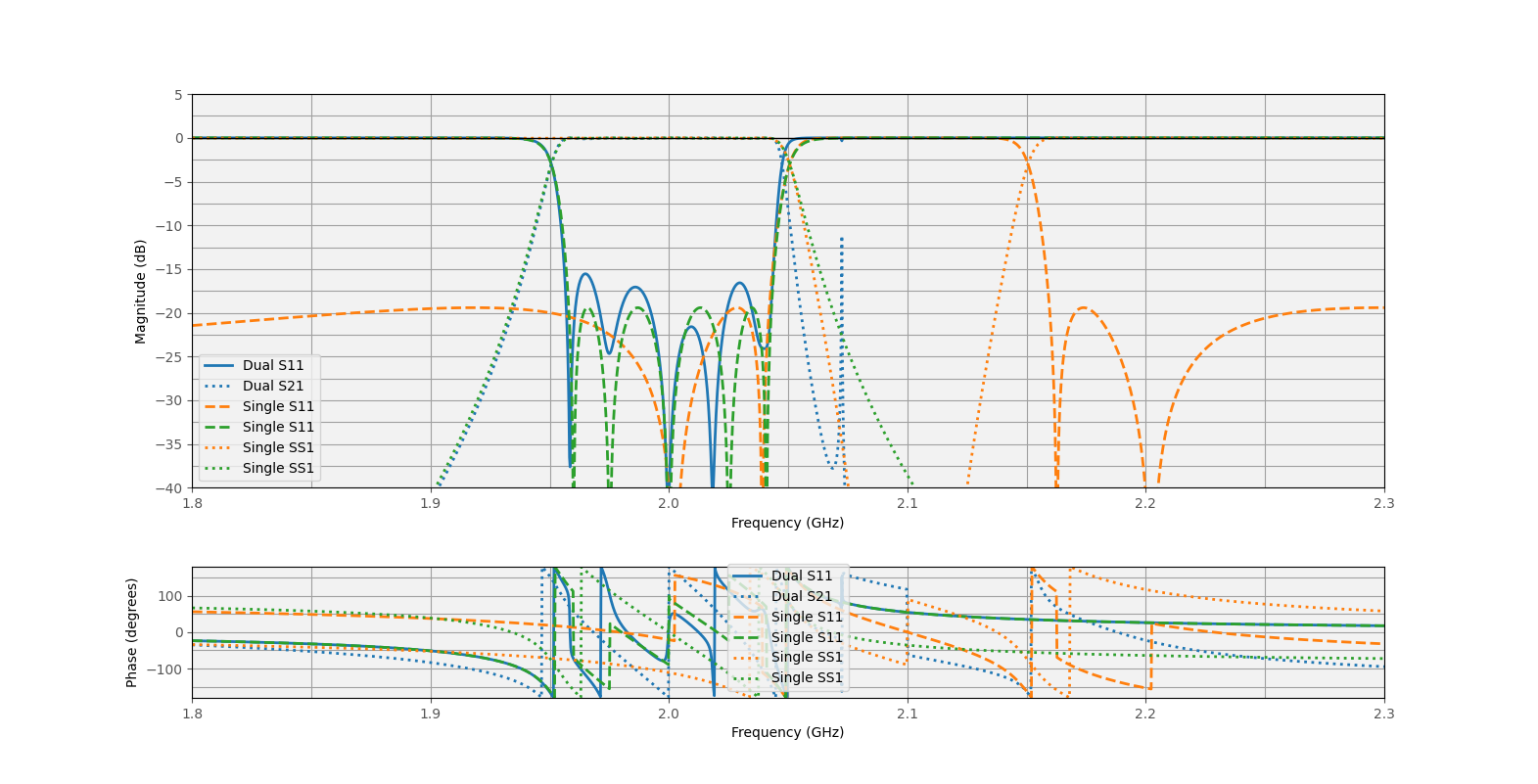
hv.plot_s_parameters(f, [S.S11, S.S21, S2.S11, S2.S21], levelindicator=-3,
labels=["Dual S11", "Dual S21", "Single S11", "Single S21"],
linestyles=["-",":","-",":"],
colorcycle=[0,0,1,1])This yields the following plot
The S-parameters of the two filter networks
It is evident from the results that the dominant stop and pass-band behavior is maintained fairly well. In fact, one can reason quite easily that in situations of total suppression, it does not really matter what is behind a filter as a signal in principle cannot reach it due to being blocked by the filter. We will later see that this is not entirely true!
In the pass band of the first 2GHz and at the stopband of the second filter, the second filter generally gets to do its job because the first filter is mostly transparent. It is mostly in the regions where the return-loss of both filters are at the same level that the internal reflections start to create strange behavior. Indeed we can see that around 2.4GHz to 2.5GHz, the return-loss is no longer at around -20dB but instead increases to around -15dB.
We can see that its mostly the pass-band behavior that is no longer guaranteed to behave as expected. In this case also, the two filters were separated in frequency by quite some amount.
We can setup another case where we have a bandpass filter at 2GHz and a band-stop filter at 2.1GHz with both a bandwidth of 100MHz. In this setup I also increased the transmission line length in between the filter to 20mm. In this case we can clearly see the degradation of the passband ripple. Furthermore, there is a spike in the stopband where the two filters try to both attenuate the signal. This stop-band spike occurs at 2.0725GHz where the return-loss increases to -10dB.
The combined behavior of two cascaded filters (bandpass and bandstop)
Why does this happen?
Looking at the dotted lines representing the S21 of both filters, we see that this spike occurs in a region where both filters attempt to attenuate by a comparable amount. Because these are reflective filters, we see high reflections in between the two filters causing resonance effects in the transmission line. But why does that lead to this behavior?
We know from microwave theory that transmission lines introduce a rotation of the load impedance around the Smiths chart. Especially if that transmission-line is not well matched and long, the load impedance corresponding to the band stop filter will start to spiral aggressively around the origin of the Smith’s chart.
A filter operates effectively as an impedance transformer in its rejection band that makes an otherwise matched load look like something entirely different. In this case the stopband filter transforms the 50 ohm load impedance of port two and the first passband filter transforms the load impedance of the band-stop filter transformed by the transmission line. The introduced rotation by the transmission line this rotation will increase the chance that the load impedance of the band-stop filter looks like 50Ohms through the band-pass filter.
The band-pass filter thus “matches” the mismatched band-stop filter. Matches is a strong word because the reflection coefficient is still very high but certainly not as close to 0dB and we definitely do not get the low suppression we hoped for.
An attentive reader might question the earlier claim that the second filter cannot affect the first because the signal cannot reach it. If that is the case, how can the second filter nearly undo the effects of the first?
The explanation lies in the fact that a filter never completely eliminates a signal. A small residual signal manages to pass through the first filter and reflects off the second, initiating resonance between the two filters. This resonance generates a high-voltage standing wave in the transmission line between them. Higher voltages produce higher currents, effectively reducing the apparent impedance from the perspective of the voltage attempting to drive a current into the first filter.
Consider an analogy: two voltage sources connected in series with a load. The addition of the second source increases the total current through the circuit. To each source, this increased current makes the load impedance appear lower, even though the sources are unaware of their mutual contribution. Similarly, the standing wave between the filters, under the right conditions, draws more energy through the first filter than expected. The resonant structure amplifies the total voltage, forcing greater current flow through both filters.
What can we do?
One way of preventing this from happening is by decreasing the distance between these two filters and thus minimizing the chances that the two filters match each other. Another more reliable option is to add an an isolator to prevent the resonance between the two filters. Isolators however do add much more complexity to your circuit and cost and often cannot be implemented with a small footprint.
Another option may be to add significant level of attenuation in between the two filters. Simply adding a loss tangent of 0.5 to the transmission line to model the effects of attenuation will remove the resonance but also increase your total transmission loss in the pass band by almost 3dB.
In conclusion
If you thought this blog post was a lesson about filter cascading you are correct but also not really. It is also a shameless way of me showing how easily one can setup these simple experiments using my Python module Heavi!
Not every circuit simulation has to be of perfect quality. Sometimes we just want to run experiments to build intuitions on the behavior of components in certain conditions. Being able to do away with all the steps of programs like ADS to setup and run simulations can help you quickly get to the answer you need!